Answer:
a. 2x³
b. 2
c. 3
d. As x → -∞, f(x) → -∞. As x → ∞, f(x) → ∞.
e. (-0.4, 13.6) and (2.8, -18.6).
f. (-1.5, 0), (1, 0), (4, 0)
g. (0, 12)
h. See attachment.
Explanation:
Given polynomial:
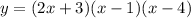
Leading term and Leading coefficient
The given polynomial is in factored form.
To find the leading term and the leading coefficient, simply multiply the variable terms of the factors:
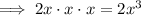
Therefore:
- Leading term = 2x³
- Leading coefficient = 2
Degree of the polynomial
The degree of the polynomial is the exponent of the leading term.
Therefore, the degree of the given polynomial is 3.
End behaviour
As the degree of the polynomial is odd and the leading coefficient is positive, the end behaviour of the function is:
- As x → -∞, f(x) → -∞
- As x → ∞, f(x) → ∞
Turning points
The x-values of the turning points are when the derivative of the function equals zero.
Expand the polynomial:


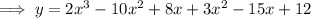
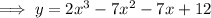
Differentiate:
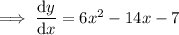
Set it to zero and solve for x:
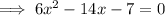
Solve using the quadratic formula:

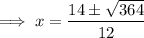

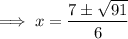
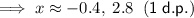
Substitute the found values of x into the original polynomial to find the y-values of the turning points:
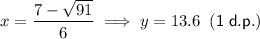
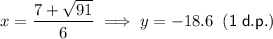
Therefore, the turning points of the polynomial (to the nearest tenth) are:
- (-0.4, 13.6) and (2.8, -18.6)
x-intercepts
The x-intercepts are when the function equals zero.
As the function is already in factored form, simply equal each of the factors to zero and solve for x:
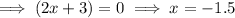
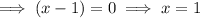

Therefore, the x-intercepts are:
- (-1,5, 0), (1, 0), (4, 0)
y-intercept
The y-intercept when x = 0:
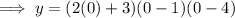
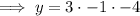
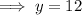
Therefore, the y-intercept is:
Sketch the graph
To sketch the graph:
- Plot the x-intercepts (-1.5, 0), (1, 0) and (4, 0).
- Plot the y-intercept (0, 12).
- Plot the turning points (-0.4, 13.6) and (2.8, -18.6).
- Begin the curve in quadrant III, pass through the first x-intercept to the first turning point.
- Change direction, pass through the y-intercept, the second x-intercept and to the second turning point.
- Change direction, pass through the third x-intercept and continuing towards ∞ in quadrant I.