Answer:
B. 6 units
Explanation:
Given equations:
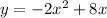
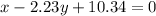
The points at which the rod is attached to the archway are the points of intersection of the two equations.
Rearrange the second equation to make x the subject:
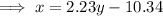
Substitute this into the first equation to create a quadratic:
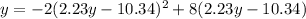
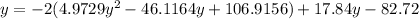

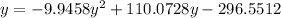
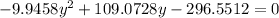

Solve the quadratic using the quadratic formula:
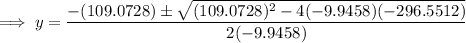
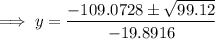
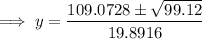
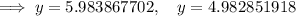
As point B is at a higher level than point A, the y-value of point B is approximately 6 units.
Therefore, point B is 6 units from ground level.