Question

A toy rocket is shot vertically into the air from a launching pad 7 feet above the ground with an initial velocity of 72 feet per second. The height h, in feet, of the rocket above the ground at t seconds after launch is given by the function h(t)=-16 t²+72 t+7. How long will it take the rocket to reach its maximum height? What is the maximum height?

The rocket reaches its maximum height at ? second(s) after launch.
(Simplify your answer.)
The maximum height reached by the object is ? feet.
(Simplify your answer.)

Answer 1

The rocket reaches its maximum height at 2.25 second(s) after launch.

The maximum height reached by the object is 88 feet.

Explanation:

How long will it take the rocket to reach its maximum height?

h(t)=-16t² + 72t +7 is a quadratic equation in the form at²+bt+c, where a=-16 and b=72 and c=7.

The maximum height would be at the vertex / peak of this equation, and we can find the x-coordinate (aka the value of 't') at this point using the formula
`(-b)/(2a)`:

`t=(-b)/(2a) =(-72)/(2(-16)) =(72)/(32) =2.25seconds`

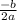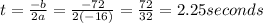
What is the maximum height?

Since we know how long it takes to reach maximum height, we can sub this value into the equation to find our answer:

h(t)=-16t² + 72t +7

h(2.25)=-16(2.25)² + 72(2.25) +7

=-81+162+7=88feet