Answer:
13. 7.5 square units
14. 24.5 square units
Explanation:
Question 13
Given vertices:
- E = (3, 1)
- F = (3, -2)
- G = (-2, -2)
As points E and F share the same x-value and points F and G share the same y-value, the polygon is a right triangle with base GF and height FE.
As points F and G share the same y-value, the length of line segment GF is the difference between the x-values:
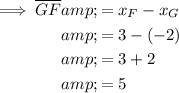
As points E and F share the same x-value, the length of line segment FE is the difference between the y-values:
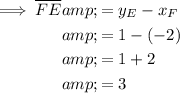
Therefore, the area of polygon EFG is:

Question 14
Given vertices:
- J = (-3, 4)
- K = (4, 4)
- L = (3, -3)
As points J and K share the same y-value the polygon is a triangle with base JK and height of the difference in y-values of points K and L.
As points J and K share the same y-value, the length of line segment JK is the difference between the x-values:
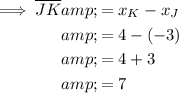
The height of the triangle is the difference between the y-values of points K and L:
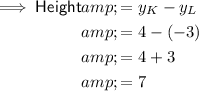
Therefore, the area of polygon JKL is:
