Question

F(x) = 2x² -

-x-1
(a) Is the point (-2,9) on the graph of f?
(b) If x=2, what is f(x)? What point is on the graph of f?
(c) If f(x) = -1, what is x? What point(s) are on the graph of f?
(d) What is the domain of f?
(e) List the x-intercept(s), if any, of the graph of f.
(f) List the y-intercept, if there is one, of the graph of f.

Answer 1

Explanation:

a. Plug in -2 for x and 9 for f(x)

`9 = 2( - 2) {}^(2) - ( - 2) - 1`

`9 = 8 + 2 - 1`

`9 = 9`

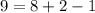
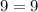
Yes, the point is on the graph.

Plug in 2 for x and solve for y.

`2(2) {}^(2) - 2 - 1 = 5`

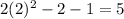
The points on there is (2,5)

c. Plug in -1 for y, solve for x.

`- 1 = 2 {x}^(2) - x - 1`

`0 = 2 {x}^(2) - x`

`0 = x(2x - 1)`

`x = 0`

`0 = 2x - 1`

`x = (1)/(2)`

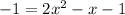
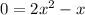
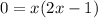
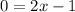
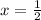
The points on the graph are (1/2,-1) and (0,-1)

d. The domain of any quadratic is all real numbers or (-oo, oo)

e.

`2 {x}^(2) - x - 1 = 0`

`2 {x}^(2) - 2x + x - 1 = 0`

`2x(x - 1) + 1(x - 1) = 0`

`(2x + 1)(x - 1) = 0`

`x = - (1)/(2)`

`x = 1`

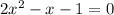
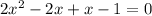
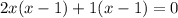
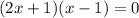
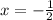
The x intercepts are -0.5,1

The y intercepts are -1