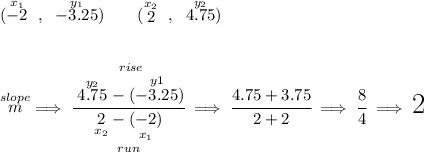to get the slope of any straight line, we simply need two points off of it.
so from what I can tell in the graph, check the picture below, the line goes above the 4 about 3/4 pretty much, or namely 0.75 above the 4, that'd make it 4.75, the graph also goes below the -3, about 1/4 below, namely 0.25 that'd make it -3.25, because two grid lines make up a whole number, so let's use those two points to get its slope.