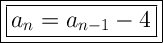Answer:
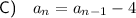
Explanation:
The plotted (n, a(n)) points on the given graph are:
- (1, 13)
- (2, 9)
- (3, 5)
- (4, 1)
- (5, -3)
From observation of these points, we can see that each successive term is obtained by subtracting 4 from the previous term. As there is a constant difference between terms, the sequence is arithmetic.
A recursive rule for an arithmetic sequence is a formula that generates each term in the sequence based on the previous term and a common difference.
The general formula for a recursive arithmetic sequence is:
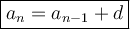
where:
 is the nth term in the sequence.
is the nth term in the sequence.
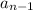 is the previous term (the term before ).
is the previous term (the term before ).- d is the common difference.
Since the common difference between terms is -4, the recursive rule for the sequence shown in the graph is: