Question

Two students in different classes took the same math test. Both students received a

score of 87. In student A's class the mean was 78 and the standard deviation of 5. In
student B's class the mean was 76 with a standard deviation of 4. Which student
scored in the top 10% of their class?

Answer 1

Both students scored in the top 10% of their classes.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
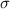`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

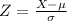
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

In this question:

Top 10% = Above the 100 - 10 = 90th percentile.

The 90th percentile of scores is X when Z has a pvalue of 0.9, that is, Z = 1.28.

So, the student who had a z-score above 1.28 scored in the 90th percentile of their class.

In student A's class the mean was 78 and the standard deviation of 5. He scored 87.

We have that
`\mu = 78, \sigma = 5, X = 87`

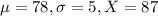
Then

`Z = (X - \mu)/(\sigma)`

`Z = (87 - 78)/(5)`

`Z = 1.8`

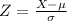
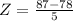
1.8 > 1.28, so student A scored in the top 10% of his/her class.

Student B's class the mean was 76 with a standard deviation of 4. Scored 87.

We have that
`\mu = 76, \sigma = 4, X = 87`

Then

`Z = (X - \mu)/(\sigma)`

`Z = (87 - 76)/(4)`

`Z = 2.75`

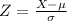
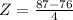
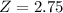
2.75 > 1.28, so student B also scored in the top 10% of his/her class.

Both students scored in the top 10% of their classes.