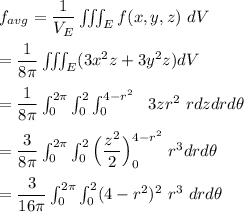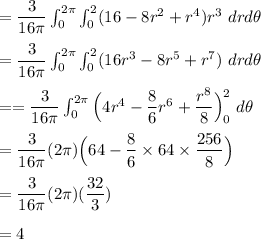Question

The average value of a function f(x, y, z) over a solid region E is defined to be fave = 1 V(E) E f(x, y, z) dV where V(E) is the volume of E. For instance, if ???? is a density function, then ????ave is the average density of E. Find the average value of the function f(x, y, z) = 3x2z + 3y2z over the region enclosed by the paraboloid z = 4 − x2 − y2 and the plane z = 0.

Answer 1

The average function
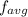`f_(avg)` value = 4

Explanation:

Given that:

`f(x,y,z) = 3x^2z+3y^2z`

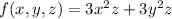
The enclosed region
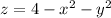`z = 4 -x^2 -y^2` and the plane z = 0.

Over an area E, the average value of a function f(x,y,z) is:

`f_(avg) = (1)/(V_(E)) \iiint_E f(x,y,z) dV ------ (1)`

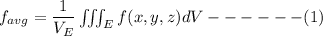
where;

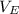`V_E` = volume of region E

To find the volume use cylindrical coordinates;

`x=rcos \theta; \ \ \ y = rsin \theta; \ \ \ z = z`

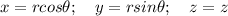
Then;

E = 0 ≤ r ≤2, 0 ≤ θ ≤ 2π, 0 ≤ z ≤ 4 - r²

`V_E = \int^(2 \pi)_(0) \int^(2)_(0) \int^(4-r^2)_(0) \ rdzdrd \theta`

`V_E = \int^(2 \pi)_(0) \int^(2)_(0) r(4-r^2) \ drd \theta`

`V_E = \int^(2 \pi)_(0) \int^(2)_(0) (4r-r^3) \ drd \theta`

`V_E = \int^(2 \pi)_(0) \Big(2r^2- (r^4)/(4) \Big)^2_0 \ d \theta`

`V_E = 4(2 \pi)\\\\ V_E = 8 \pi`

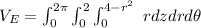
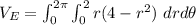
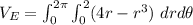
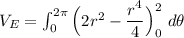
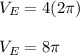
However, from equation (1):

`f_(avg) = (1)/(V_E) \iiint_E f(x,y,z) \ dV \\ \\ = (1)/(8 \pi) \iiint_E (3x^2z + 3y^2 z) dV \\ \\ = (1)/(8 \pi ) \int^(2 \pi)_(0) \int^(2 )_(0) \int^(4 - r^2)_(0) \ \ 3zr^2 \ rdzdrd\theta \\ \\ = (3)/(8 \pi) \int^(2 \pi)_(0) \int^(2 )_(0) \Big((z^2)/(2)\Big)^(4-r^2)_(0) \ r^3 drd\theta \\ \\ = (3)/(16 \pi) \int^(2 \pi)_(0) \int^(2 )_(0) (4-r^2)^2 \ r^3 \ dr d\theta`

`= (3)/(16 \pi) \int^(2 \pi)_(0) \int^(2 )_(0) (16-8r^2 + r^4)r^3 \ dr d\theta \\ \\ = (3)/(16 \pi) \int^(2 \pi)_(0) \int^(2 )_(0) (16r^3 -8r^5 + r^7) \ dr d \theta \\ \\ = = (3)/(16 \pi) \int^(2 \pi)_(0) \Big (4r^4 - (8)/(6)r^6 + (r^8)/(8) \Big)^2_0 \ d \theta \\ \\ = (3)/(16 \pi ) (2 \pi) \Big (64 - (8)/(6) * 64 * (256)/(8) \Big) \\ \\ = (3)/(16 \pi) (2 \pi) ((32)/(3)) \\ \\ = 4`