Question

You have collected weekly earnings and age data from a sub-sample of 1,744 individualsusing the Current Population Survey in a given year. Given the overall mean of $434.49and a standard deviation of $294.67, construct a 99% confidence interval for averageearnings in the entire population. State the meaning of this interval in words, ratherthan just in numbers. If you constructed a 90% confidence interval instead, would itbe smaller or larger? What is the intuition?

Answer 1

The 99% confidence interval for average weekly earnings in the entire population is between $416.42 and $452.66. This means that we are 99% sure that the true population mean weekly earnings is between these two values.

Due to the smaller margin of error, the confidence interval would be smaller, that is, less likely to contain the true population mean.

Explanation:

We have that to find our
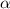`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.99)/(2) = 0.005`

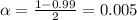
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
`1 - 0.005 = 0.995`, so Z = 2.575.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

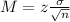
In which
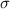`\sigma` is the standard deviation of the population and n is the size of the sample.

`M = 2.575(294.67)/(√(1744)) = 18.17`

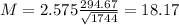
The lower end of the interval is the sample mean subtracted by M. So it is 434.49 - 18.17 = $416.42

The upper end of the interval is the sample mean added to M. So it is 434.49 + 18.17 = $452.66

The 99% confidence interval for average weekly earnings in the entire population is between $416.42 and $452.66. This means that we are 99% sure that the true population mean weekly earnings is between these two values.

If you constructed a 90% confidence interval instead, would it be smaller or larger? What is the intuition?

For a 90% confidence interval, we would have z = 1.645.

Looking at the margin of error formula, M and z are direct proportional, that is, as z decreases so does M. Due to the smaller margin of error, the confidence interval would be smaller, that is, less likely to contain the true population mean.