Question

A cone (V=1/3 pi r^ 2 h) dagger has a height of 9 inches and a volume equal to (3pi * y ^ 2 + 30pi*y + 75pi) cubic inches What is the cone's radius () in terms of y? Show all steps.

Answer 1

`√(y^2 + 10y + 25) = r`

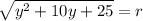
Explanation:

So we're given that the volume of a cone can be defined as:

`V=(1)/(3)\pi r^2h`

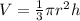
We're also given that:

`h=9 \text{ (since height = 9 inches)}`

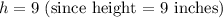
So let's substitute in that nine in to the equation:

`V=(1)/(3)\pi r^2 * 9`

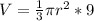
Let's simplify a bit by multiplying the 9 by 1/3 (same as dividing by 3)

`V=(9)/(3)\pi r^2\\\\V=3\pi r^2`

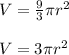
We're finally given that:

`V = 3\pi y^2 + 30\pi y + 75\pi`

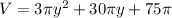
so let's use this definition and substitute it in for our volume to get:

`3\pi y^2 + 30\pi y + 75\pi = 3\pi r^2`

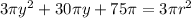
From here we want to solve for r, since we want the radius in terms of y.

So let's first divide by
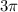`3\pi` on both sides to get rid of the coefficient.

`(3\pi y^2 + 30\pi y + 75\pi)/(3\pi) = (3\pi r^2)/(3\pi)`

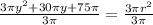
from here we can distribute the division across the terms (and simplify on the right) to get:

`(3\pi y^2)/(3\pi) + (30\pi y)/(3\pi) + (75\pi)/(3\pi) = r^2`

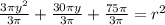
from here we can simplify the terms to get:

`y^2+10y+25=r^2`

Now the only thing that we need to remove is that square, which we can do by applying the square root to both sides of the function:

`√(y^2 + 10y + 25) = √(r^2)\\\\√(y^2 + 10y + 25) = r`

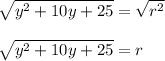
and now we're done isolating "r" and it's expressed in terms of y