Question

A bird is flying directly toward a stationary bird-watcher and emits a frequency of 1490 Hz. The bird-watcher, however, hears a frequency of 1505 Hz. What is the speed of the bird, expressed as a percentage of the speed of sound

Answer 1

The speed of the bird is 1.00% of the speed of sound.

Step-by-step explanation:

The speed of the bird can be found by using the Doppler equation:

`f = f_(0)((v - v_(r))/(v - v_(s)))`

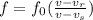
Where:

v: is the speed of sound = 343 m/s

f₀: is the frequency emitted = 1490 Hz

f: is the frequency observed = 1505 Hz

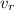`v_(r)`: is the speed of the receiver = 0 (it is stationary)

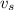`v_(s)`: is the speed of the source =?

The minus sign of
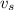`v_(s)` is because the source is moving towards the receiver.

By solving the above equation for
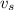`v_(s)` we have:

`v_(s) = v - (f_(0)*v)/(f) = 343 - (1490*343)/(1505) = 3.42 m/s`

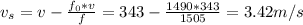
The above speed in terms of the speed of sound is:

`\% v_(s) = (3.42)/(343)* 100 = 1.00 \%`

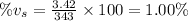
Therefore, the speed of the bird is 1.00% of the speed of sound.

I hope it helps you!