Answer:
K_f = 1881.6 J
Step-by-step explanation:
To solve this exercise, let's start by finding the velocities of the bodies.
We define a system formed by the initial object and its parts, with this the forces during the explosion are internal and the moment is conserved
initial instant. Before the explosion
p₀ = M v₀
final instant. After the explosion
p_f = m₁ v + m₂ 0
the moeoto is preserved
p₀ = p_f
M v₀ = m₁ v
v =
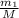 v₀
v₀
in the exercise they indicate that the most massive part has twice the other part
M = m₁ + m₂
M = 2m₂ + m₂ = 3 m₂
m₂ = M / 3
so the most massive part is worth
m₁ = 2 M / 3
we substitute
v = ⅔ v₀
with the speed of each element we can look for the kinetic energy
initial
K₀ = ½ M v₀²
Final
K_f = ½ m₁ v² + 0
K_f = ½ (⅔ M) (⅔ v₀)²
K_f =
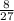 (½ M v₀²)
(½ M v₀²)
K_f =
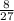 K₀
K₀
the energy added to the system is
ΔK = Kf -K₀
ΔK = (8/27 - 1) K₀
ΔK = -0.7 K₀
K_f = K₀ + ΔK
K_f = K₀ (1 -0.7)
K_f = 0.3 K₀
let's calculate
K_f = 0.3 (½ 64 14²)
K_f = 1881.6 J