Answer:
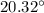 and
and
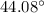
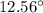 and
and
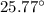
Step-by-step explanation:
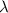 = Wavelength
= Wavelength
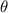 = Angle
= Angle
m = Order
Distance between grating is given by
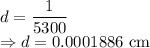
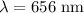
We have the relation
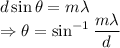
m = 1
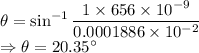
m = 2
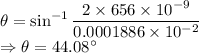
The first and second order angular deflection is
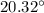 and
and
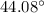
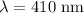
m = 1
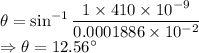
m = 2
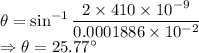
The first and second order angular deflection is
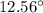 and
and
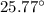 .
.