Question

In a particular region, 6% of the population is thought to have a certain disease. A standard diagnostic test has been found to correctly identify 91% of the people who have the disease. However, the test also incorrectly diagnoses 8% of those who do not have the disease as having the disease (in other words, the person does not have the disease but the test tells them that they do). A randomly selected person in the region is tested for the disease. (a) What is the probability the test comes back positive

Answer 1

The positive predictive value ≈ 30.012%

Explanation:

(a) The given percentage of the people in the region that have the disease, P(D) = 6% = 0.06

The percentage people correctly identified as having the disease by the standard diagnostic test = 91%

The percentage of people incorrectly identified as having the disease by the standard diagnostic test, P(T + |H) = 8%

Therefore, the sensitivity of the test, P(T + |D) = 0.91

The specificity of the test, P(T - |H) = 1 - 0.08 = 0.92

Therefore, the probability that a person is healthy, P(H) = 1 - 0.06 = 0.94

Therefore, in a population of 1,000 people, 60 people have the disease, with a sensitivity of 91%, the test will correctly pic 0.91×66 = 60.06 people correctly with the disease and 0.91 × 940 = 855.4 people without the disease

The number of non-diseased that test positive by the test is 0.08 × 1000 = 80 people which are false positives

Therefore, the number of diseased diagnosed as negative is 0.08 × 60 = 4.8

Therefore, we have;

`\begin{array}{cccc}&Deseased&Non-diseased& Diseased + Non-diseased\\Test \ +ve&60.06&80& 140.06\\Test \ -ve&4.8&855.4&\end{array}`

The positive predictive value = Diseased +ve/(Diseased +ve + Non-diseased +ve)

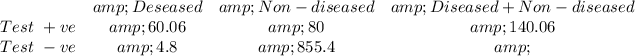
`The \ positive \ predictive \ value = (Diseased +ve)/(Diseased +ve + Non-diseased +ve) * 100`

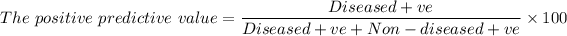
Therefore;

The positive predictive value = 60.06/(60.06 + 140.06) × 100 ≈ 30.012%