Answer:
(a) V = 300r -πr³ cm³
(b) r = √(100/π) cm
(c) p ≈ 6.5 cm
Explanation:
Given a cylinder with a surface area of 600 cm², you want to show (a) that its volume is V=300r -πr³, and (b) that the radius for maximum volume is r=√(100/π). You also want to find the radius of a sphere with that same maximum volume.
Formulas
The formulas for the area and volume of a cylinder and the radius of a sphere are ...
A = 2πr(r +h) . . . . . . surface area of a cylinder of radius r, height h
V = πr²h . . . . . . . . . volume of a cylinder of radius r, height h
r = ∛(3V/(4π)) . . . . radius of a sphere with volume V
(a) cylinder volume
Solving the cylinder surface area formula for height, we get ...
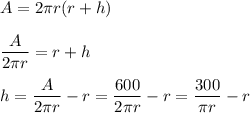
Using this value in the volume formula, we find the cylinder volume to be ...
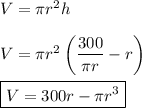
(b) cylinder radius
The volume of the cylinder is maximized when its derivative with respect to radius is zero:
V' = 300 -3πr² = 0
100 = πr² . . . . . . . . . . divide by 3, add πr²
r = √(100/π) . . . . . . . divide by π, take the square root
The radius of the cylinder with surface area 600 cm² and maximum volume is r = √(100/π).
(c) sphere radius
The volume of the cylinder with maximum volume is ...
V = r(300 -πr²) = r(300 -100) = 200r = 200√(100/π)
V = 2000/√π
The radius of the sphere with the same volume is ...
![p=\sqrt[3]{(3V)/(4\pi)}=\sqrt[3]{(3(2000)/(√(\pi)))/(4\pi)}=\frac{\sqrt[3]{1500}}{√(\pi)}\approx6.45836\\\\\boxed{p\approx6.5\text{ cm}}](https://img.qammunity.org/2023/formulas/mathematics/college/m3xalk17x28whdhcsjjccmcdyypu34wxk9.png)