An inequality to find the times when the ball is more than 12 meters above the ground is
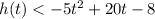 .
.
The times when the ball is more than 12 meters above the ground is 0.45 seconds < t < 3.55 seconds.
In order to find the times when the ball would attain a height that is more than 12 meters above the ground, we would have to set up an inequality as follows;
h(t) > 12 meters.
By applying the substitution method, we have the following:

where:
a = -5, b = 20, and c = -8
By solving the quadratic function using the quadratic formula, we have:

t = 2 - 1.55
t = 0.45 seconds.
t = 2 + 1.55
t = 3.55 seconds.
Therefore, the times when the ball is more than 12 meters above the ground can be written as follows;
0.45 seconds < t < 3.55 seconds.