Question

Find the exact value of csc 330° in simplest form with a rational denominator-

Answer 1

`\implies \cosec 330^o = -2`

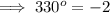
Explanation:

Given :-

• 
  `\cosec 330^o`

And we need to find out its value . Firstly we know that 330° lies in 4th quadrant . And In fourth quadrant , cosine and secant are positive and the rest are negative .So cosecant will be negative . Therefore , the result will be -ve. Now we know that ,

`\implies \cosec (360^o-\theta)= -\cosec\theta`

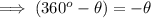
Using this ,

`\implies \cosec (330^o) \\\\\rm\implies cosec(360^o-30^o) \\\\\rm\implies - \cosec 30^o`

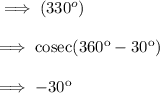
And the value of cosec 30° is ,

`\implies -\cosec 30^o = \boxed{\red{-2}}`

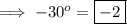
Hence the required answer is -2 .

Answer 2

The answer is -2 for the csc and it’s also a rational denominator