Question

If 30 buses can carry 1,500 people, how many people can 5 buses carry? A 200 © 500 B 250 D 750​

Answer 1

`\boxed {\boxed {\sf 250 \ people}}`

Explanation:

Let's set up a proportion using the following setup.

`\frac {buses}{people}=\frac {buses}{people}`

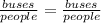
We know 30 buses can carry 1,500 people.

`\frac {30 \ buses}{1500 \ people}=\frac {buses}{people}`

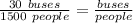
We don't know how many people 5 buses can carry, so we say 5 buses carry x people.

`\frac {30 \ buses}{1500 \ people}=\frac {5 \ buses}{x \ people}`

`\frac {30 }{1500 }=\frac {5 }{x }`

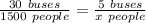
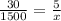
Cross multiply. Multiply the numerator of the first fraction by the second fraction's denominator. Then, multiply the first denominator by the second numerator.

`30*x=1500*5\\30x=7500`

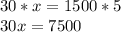
Solve for x. It is being multiplied by 30. The inverse of multiplication is division. Divide both sides by 30.

`30x/30=7500\\x=250`

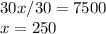
5 buses can carry 250 people.