Question

The volume of a box, a rectangular prism, is represented by the function f(x) = x³ + x²-17x + 15. The length of the box is (x + 5), and the width is (x-1). Find

the expression representing the height of the box.

Answer 1

x-3

Explanation:

(x+5)(x-1)(height)=x3+x2-17x+15

x2+5x-1x-5(h)=x2+4x-5

what times x2+4x-5 will equal the volume

look at the constant -5 and what will multiply with that to get 15 so -3 right so then check the rest of it by doing (x2+4x-5)(x-3) =x3−3x2+4x2−12x−5x+15

=x3+x2−17x+15 so the answer is x-3

Answer 2

(x - 3)

Explanation:

Given:

• 
  `\textsf{Volume}: f(x)=x^2+x^2-17x+15`

• 
  `\textsf{Length}=(x+5)`

• 
  `\textsf{Width}=(x-1)`

Substitute the given expressions for volume, length and width into the formula for volume of a rectangular prism:

`\begin{aligned}\textsf{Volume of rectangular prism} & = \sf width * length * height\\\\\implies x^3+x^2-17x+15&=(x-1)(x+5)h\\\\x^3+x^2-17x+15&=(x^2+4x-5)h\\\\h&=(x^3+x^2-17x+15)/(x^2+4x-5)\end{aligned}`

To find the height (h), carry out long division:

`\large \begin{array}{r}x-3\phantom{)}\\x^2+4x-5{\overline{\smash{\big)}\,x^3+x^2-17x+15\phantom{)}}}\\{-~\phantom{(}\underline{(x^3+4x^2-5x)\phantom{-b..)}}\\-3x^2-12x+15\phantom{)}\\-~\phantom{()}\underline{(-3x^2-12x+15)\phantom{}}\\0\phantom{)}\\\end{array}`

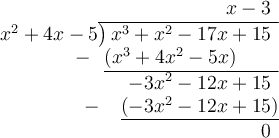
Therefore, the expression that represents the height of the box is (x - 3).