Question

Please help me solve this and also please show me the work :)

Answer 1

Given:

The figure of a right triangle.

To find:

All the six trigonometric ratios for the angle θ.

Solution:

Using the Pythagoras theorem, we get

`Hypotenuse^2=Perpendicular^2+Base^2`

`Hypotenuse^2=(9)^2+(12)^2`

`Hypotenuse^2=81+144`

`Hypotenuse^2=225`

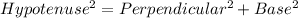
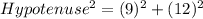
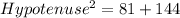
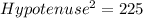
Taking square root on both sides, we get

`Hypotenuse=15`

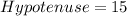
Now, the six trigonometric ratios for the angle θ are:

`\sin\theta=(Perpendicular)/(Hypotenuse)`

`\sin\theta=(12)/(15)`

`\sin\theta=(4)/(5)`

`\cos\theta=(Base)/(Hypotenuse)`

`\cos\theta=(9)/(15)`

`\cos\theta=(3)/(5)`

`\tan\theta=(Perpendicular)/(base)`

`\tan\theta=(12)/(9)`

`\tan\theta=(4)/(3)`

`\csc\theta=(1)/(\sin \theta)`

`\csc\theta=(1)/((4)/(5))`

`\csc\theta=(5)/(4)`

`\sec\theta=(1)/(\cos \theta)`

`\sec\theta=(1)/((3)/(5))`

`\sec\theta=(5)/(3)`

`\cot\theta=(1)/(\tan \theta)`

`\cot\theta=(1)/((4)/(3))`

`\cot\theta=(3)/(4)`

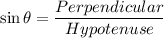
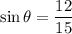
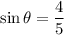
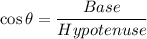
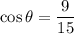
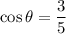
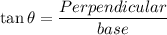
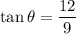
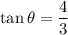
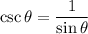
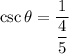
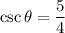
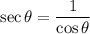
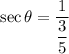
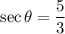
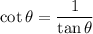
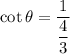
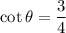
Therefore, the six trigonometric ratios are
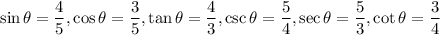`\sin\theta=(4)/(5),\cos\theta=(3)/(5),\tan\theta=(4)/(3),\csc\theta=(5)/(4),\sec\theta=(5)/(3),\cot\theta=(3)/(4)`.