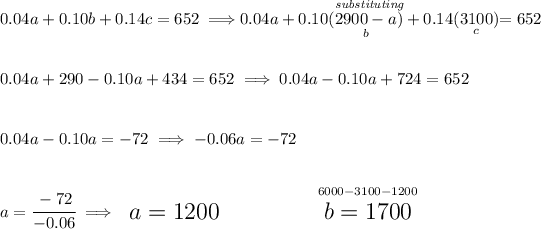Question

A person invested ​$6000 for 1​ year, part at 4​%, part at 10​%, and the remainder at 14​%. The total annual income from these investments was ​$652. The amount of money invested at ​14% was ​$200 more than the amounts invested at ​4% and 10​% combined. Find the amount invested at each rate.

Answer 1

a = amount invested at 4%

how much is 4% of "a"? (4/100) * "a", namely 0.04a.

b = amount invested at 10%

how much is 10% of "b"? (10/100) * "b", namely 0.10b.

c = amount invested at 14%

how much is 14% of "c"? (14/100) * "c", namely 0.14c.

we know the total amount invested is 6000, so whatever "a" and "b" and "c" might be, we know that a + b +c = 6000.

we also know that the yielded amount in interest is $652, so if we simply add their interest, that'd be 0.04a + 0.10b + 0.14c.

the combined amount of "a" and "b" is simply a + b, and we also know that "c" is that much plus 200, namely "c = a + b + 200".

`a+b+c=6000\hspace{5em}\underline{c=a+b+200} \\\\\\ a+b+\stackrel{c}{(a+b+200)}=6000\implies 2a+2b+200=6000\implies 2a+2b=5800 \\\\\\ 2b=5800-2a\implies b=\cfrac{5800-2a}{2}\implies \boxed{b=2900-a} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{since we know that}}{c=a+b+200}\implies \stackrel{substituting}{c=a+(\underset{b}{2900-a})+200}\implies c=a+2900-a+200 \\\\\\ c=2900+200\implies {\Large \begin{array}{llll} c=3100 \end{array}} \\\\[-0.35em] ~\dotfill`

`0.04a+0.10b+0.14c=652\implies \stackrel{\textit{substituting}}{0.04a+0.10(\underset{b}{2900-a})+0.14(\underset{c}{3100})}=652 \\\\\\ 0.04a+290-0.10a+434=652\implies 0.04a-0.10a+724=652 \\\\\\ 0.04a-0.10a=-72\implies -0.06a=-72 \\\\\\ a=\cfrac{-72}{-0.06}\implies {\Large \begin{array}{llll} a=1200 \end{array}} \hspace{5em} \stackrel{6000-3100-1200}{{\Large \begin{array}{llll} b=1700 \end{array}}}`