Question

An alpha particle (α), which is the same as a helium-4 nucleus, is momentarily at rest in a region of space occupied by an electric field. The particle then begins to move. Find the speed of the alpha particle after it has moved through a potential difference of â3.45Ã10^â3 V .The charge and the mass of an alpha particle are qα = 3.20Ã10^â19 C and mα = 6.68Ã10â27 kg , respectively.

Mechanical energy is conserved in the presence of which of the following types of forces?

a. electrostatic
b. frictional
c. magnetic
d. gravitational

Answer 1

Speed = 575 m/s

Mechanical energy is conserved in electrostatic, magnetic and gravitational forces.

Step-by-step explanation:

Given :

Potential difference, U =
`$-3.45 * 10^(-3) \ V$`

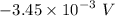
Mass of the alpha particle,
`$m_(\alpha) = 6.68 * 10^(-27) \ kg$`

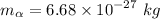
Charge of the alpha particle is,
`$q_(\alpha) = 3.20 * 10^(-19) \ C$`

So the potential difference for the alpha particle when it is accelerated through the potential difference is

`$U=\Delta Vq_(\alpha)$`

And the kinetic energy gained by the alpha particle is

`$K.E. =(1)/(2)m_(\alpha)v_(\alpha)^2 $`

From the law of conservation of energy, we get

`$K.E. = U$`

`$(1)/(2)m_(\alpha)v_(\alpha)^2 = \Delta V q_(\alpha)$`

`$v_(\alpha) = \sqrt{(2 \Delta V q_(\alpha))/(m_(\alpha))}$`

`$v_(\alpha) = \sqrt{(2(3.45 * 10^(-3 ))(3.2 * 10^(-19)))/(6.68 * 10^(-27))}$`

`$v_(\alpha) \approx 575 \ m/s$`

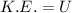
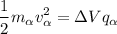
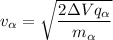
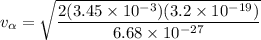
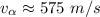
The mechanical energy is conserved in the presence of the following conservative forces :

-- electrostatic forces

-- magnetic forces

-- gravitational forces