Question

We wish to estimate what percent of adult residents in a certain county are parents. Out of 100 adult residents sampled, 8 had kids. Based on this, construct a 99% confidence interval for the proportion p of adult residents who are parents in this county. Express your answer in tri-inequality form. Give your answers as decimals, to three places.

Answer 1

0.0101 < p < 0.1499

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
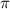`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

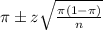
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

Out of 100 adult residents sampled, 8 had kids. Based on this, construct a 99%.

This means that
`n = 100, \pi = (8)/(100) = 0.08`

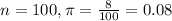
99% confidence level

So
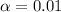`\alpha = 0.01`, z is the value of Z that has a pvalue of
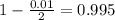`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

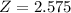The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.08 - 2.575\sqrt{(0.08*0.92)/(100)} = 0.0101`

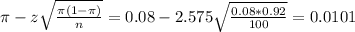
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.08 + 2.575\sqrt{(0.08*0.92)/(100)} = 0.1499`

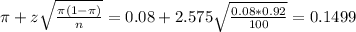
Express your answer in tri-inequality form.

0.0101 < p < 0.1499