Answer:
Approximately
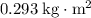 .
.
Step-by-step explanation:
Since the wheel started from rest, initial angular velocity will be
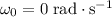 . It is given that the angular velocity
. It is given that the angular velocity
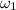 is
is
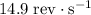 after
after
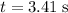 . Apply unit conversion and ensure that all angular velocity are measured in radians-per-second:
. Apply unit conversion and ensure that all angular velocity are measured in radians-per-second:
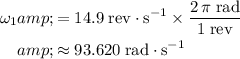 .
.
Change in angular velocity:
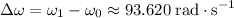 .
.
Since the tangential force is constant and there is no friction on the wheel, the angular acceleration
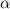 of this wheel will be constant. Since the change in velocity
of this wheel will be constant. Since the change in velocity
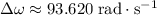 was achieved within
was achieved within
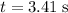 , the average angular acceleration will be:
, the average angular acceleration will be:
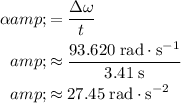 .
.
At a distance of
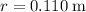 from the axis of rotation, the tangential force
from the axis of rotation, the tangential force
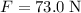 will exert on the wheel a torque
will exert on the wheel a torque
 of magnitude:
of magnitude:
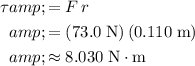 .
.
Let
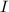 denote the moment of inertia of this wheel. The equation
denote the moment of inertia of this wheel. The equation
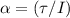 relates angular acceleration
relates angular acceleration
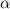 to moment of inertia
to moment of inertia
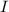 and net torque
and net torque
 . Rearrange this equation to find the moment of inertia:
. Rearrange this equation to find the moment of inertia:
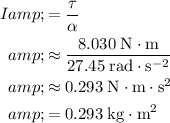 .
.
Note that the unit "radians" is typically ignored. Additionally,
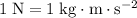 .
.
Hence, the moment of inertia of this wheel is approximately
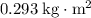 .
.