Question

The equation g(t)=2+23.7t−4.9t2 models the height, in meters, of a pumpkin t seconds after it has been launched from a catapult. Is the pumpkin still in the air 8 seconds later? Explain or show how you know.

Answer 1

The pumpkin is not in the air

Explanation:

The equation is

`g(t)=2+23.7t-4.9t^2`

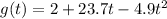
Let us find when the pumpkin will reach the ground

`0=2+23.7t-4.9t^2\\\Rightarrow -49t^2+237t+20=0\\\Rightarrow t=(-237\pm √(237^2-4\left(-49\right)* 20))/(2\left(-49\right))\\\Rightarrow t=-0.08,4.91`

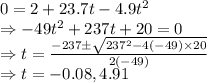
So, the pumpkin will reach the ground at 4.91 seconds. Hence, at 8 seconds the pumpkin will reach the ground.

OR

At
`t=8\ \text{s}`

`g(8)=2+23.7* 8-4.9* 8^2\\\Rightarrow g(8)=-122\ \text{m}`

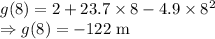
The height of the pumpkin is negative 122 m. This means it is lower than the ground. So, the pumpkin is not in the air 8 seconds later.