Question

A quantum dot may be modeled as an electron in a spherical well with perfectly reflecting walls. Design a quantum dot whose characteristic frequency of emission is 10 GHz, where characteristic frequency corresponds to decay from the first excited state to the ground state. In other words, obtain the radius a of the spherical cavity that has this property

Answer 1

radius = 37.69 mm

Step-by-step explanation:

Calculate the radius a of the spherical cavity that has this property

Frequency of emission = 10 GHz

This problem is similar to infinite spherical wall potential

first step:

Express the energy eigenvalue of the system :
`E_(100) =E_(Is) = (9.87h^2)/(2ma^2)`

First excited state energy can be expressed as : E
`_(IP)` = 20.19 h^2 / 2ma^2

Given that the frequency of emission (γ ) = 10 GHz

next step :

calculate the energy of emitted photon ( E ) = h γ

= 6.626 * 10^-36 * 10 * 10^9

= 6.626 * 10^-24 joules

E
`_(IP)` - E
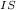`_(IS)` = 6.626 * 10^-24

∴ a^2 = 1.42 * 10^-13 m^2

hence a = √ 1.42 * 10^-13 m^2 = 37.69 * 10^-6 m ≈ 37.69 mm