Question

Sum and Product of Two Numbers Find two numbers whose sum is 20 and whose product is the maximum possible value. (Hint: Let x be one number. Then 20 - x is the other number. Form a quadratic function by multiplying them, and then find the maximum value of the function.)

Answer 1

• The numbers are 10 and 10

Explanation:

As described in the hint:

• the numbers are x and 20 - x,
• their product is maximum possible value.

The product is:

• x(20 - x) =
• - x² + 20x

This is a quadratic expression ax² + bx + c with the leading coefficient of a = - 1, b = 20 and c = 0.

It has a maximum and no minimum value since a < 0.

The x-coordinate of the maximum is the vertex which is x = - b/2a.

The x- coordinate of the vertex is:

• x = - 20/-2 = 10

The maximum value itself is:

• - 10² + 20*10 =
• - 100 + 200 =
• 100

Answer 2

10 and 10.

`f(x)=-x^2+20x`

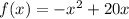
Maximum value of the function is 100.

Explanation:

Two numbers whose sum is a positive integer, and whose product is the maximum possible value have to be two positive integers.

Pairs of positive integers whose sum is 20:

• 1 and 19
• 2 and 18
• 3 and 17
• 4 and 16
• 5 and 15
• 6 and 14
• 7 and 13
• 8 and 12
• 9 and 11
• 10 and 10

The pair of numbers whose product is the maximum possible value is the pair of numbers that are closest to each other.

Therefore the pair of numbers is 10 and 10:

`\implies x = 10`

`\implies 20 - x = 10`

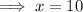
Form a quadratic function by multiplying:

`\implies f(x)=x(20-x)`

`\implies f(x)=20x-x^2`

`\implies f(x)=-x^2+20x`

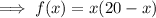
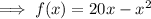
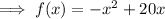
The maximum value of the function is the y-value of its vertex.

`\boxed{\begin{minipage}{5.6 cm}\underline{Vertex form of a quadratic equation}\\\\$y=a(x-h)^2+k$\\\\where:\\ \phantom{ww}$\bullet$ $(h,k)$ is the vertex. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}`

To convert the function to vertex form, complete the square.

Factor out negative 1:

`\implies f(x)=-(x^2-20x)`

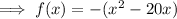
Add and subtract the square of half the coefficient of the term in x:

`\implies f(x)=-\left(x^2-20x+\left((-20)/(2)\right)^2-\left((-20)/(2)\right)^2\right)`

`\implies f(x)=-(x^2-20x+100-100)`

`\implies f(x)=-(x^2-20x+100)+100`

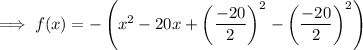
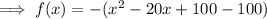
Factor the perfect square trinomial:

`\implies f(x)=-(x-10)^2+100`

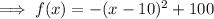
Therefore, the vertex of the function is (10, 100), and so the maximum value of the function is 100.