The equation of the line with points (0, 1) and (1, -2) is y = -3x + 1. The slope, calculated as the change in y divided by the change in x, is -3, indicating a downward slope.
To determine the equation of the line given two points,
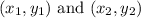 , you can use the formula for the slope m:
, you can use the formula for the slope m:
![\[ m = \frac{{y_2 - y_1}}{{x_2 - x_1}} \]](https://img.qammunity.org/2023/formulas/mathematics/college/kszl4oum5y66302rk3hbgjs5zt4b80i3ic.png)
Given the points (0, 1) and (1, -2), substitute these coordinates into the formula:
![\[ m = \frac{{(-2) - 1}}{{1 - 0}} \]](https://img.qammunity.org/2023/formulas/mathematics/college/fz3ic4x1hs2dnkag5uov8al7ggkgtwg4cn.png)
Simplify:
![\[ m = \frac{{-3}}{{1}} \]](https://img.qammunity.org/2023/formulas/mathematics/college/xjlv4qsk7hno1kplgvlf2le7l4dlegbqm0.png)
Therefore, the slope m of the line is -3. The equation of the line in point-slope form
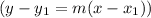 can be written using either of the given points. Let's use (0, 1):
can be written using either of the given points. Let's use (0, 1):
y - 1 = -3(x - 0)
Simplify:
y - 1 = -3x
Finally, to express it in slope-intercept form y = mx + b, add 1 to both sides:
y = -3x + 1
So, the equation of the line is y = -3x + 1 with a slope of -3.