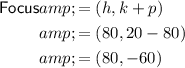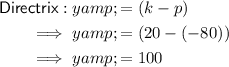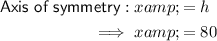Question

*PRE-CALC URGENT + 100 POINTS*

A jumping spider's movement is modeled by a parabola. The spider makes a single
jump from the origin and reaches a maximum height of 20 mm halfway across a horizontal distance of 160 mm.

Part A: Write the equation of the parabola in standard form that models the spider's jump. Show your work. (4 points)

Part B: Identify the focus, directrix, and axis of symmetry of the parabola. (6 points)

Answer 1

A. (x - 80)² = -320(y = 20)

B. Focus: (80, -60)

Directrix: y = 100

Axis of symmetry: x = 80

Explanation:

Part A

If the spider's movement is modeled by a parabola, and its maximum height is 20 mm halfway across a horizontal distance of 160 mm, then:

• x-intercepts = (0, 0) and (160, 0)
• Vertex = (80, 20)

Standard form of a parabola with a vertical axis of symmetry:

`\boxed{(x-h)^2=4p(y-k) \quad \textsf{where}\:p\\eq 0}`

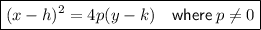
If p > 0, the parabola opens upwards, and if p < 0, the parabola opens downwards.

• 
  `\textsf{Vertex}=(h, k)`

• 
  `\textsf{Focus}=(h,k+p)`

• 
  `\textsf{Directrix}:y=(k-p)`

• 
  `\textsf{Axis of symmetry}:x=h`

Substitute one of the x-intercepts and the vertex into the formula and solve for p:

`\implies (0-80)^2=4p(0-20)`

`\implies (-80)^2=4p(-20)`

`\implies 6400=-80p`

`\implies p=-80`

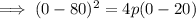
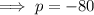
Substitute the found value of p and the vertex into the formula to create the equation of the parabola in standard form:

`\implies (x-80)^2=4(-80)(y-20)`

`\implies (x-80)^2=-320(y-20)`

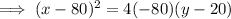
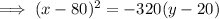
Part B

Given:

• h = 80
• k = 20
• p = -80

`\begin{aligned}\textsf{Focus}&=(h,k+p)\\&=(80,20-80)\\&=(80,-60)\end{aligned}`

`\begin{aligned}\textsf{Directrix}:y&=(k-p)\\ \implies y&=(20-(-80))\\ \implies y&=100\end{aligned}`

`\begin{aligned}\textsf{Axis of symmetry}:x&=h\\ \implies x&=80\end{aligned}`