Given:
The vertex of a quadratic function is (-5,-1) and it passes through the point (-2,2).
To find:
The vertex and standard form of the quadratic function.
Solution:
The vertex form of a quadratic function is:

Where, a is a constant, (h,k) is vertex.
The vertex of a quadratic function is (-5,-1). It means
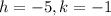 .
.
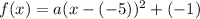
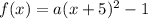 ...(i)
...(i)
The quadratic function passes through the point (-2,2). Putting
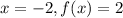 in (i), we get
in (i), we get
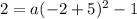
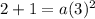
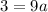
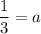
Putting
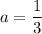 in (i), we get
in (i), we get
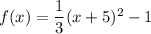
Therefore, the vertex for of the quadratic function is
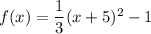 .
.
The standard form of a quadratic function is:
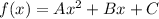
We have,
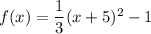
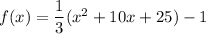
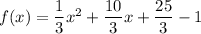
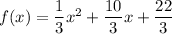
Therefore, the standard form of a quadratic function is
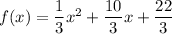 .
.