Question

Solve picture pls thanks

Answer 1

m∠1 = 30°

m∠2 = 120°

m∠3 = 30°

w = 52

x = 104 (approximately)

y = 156 (approximately)

z = 180

Explanation:

Step 1: Label your diagram with variables to make solving easier

Step 2: Solve for the missing degrees

• *Note: A triangle adds up to 180°
• m∠1 = 180° - 90° - 60° = 30°
• *Note: A line adds up to 180°
• m∠2 = 180° - 60° = 120°
• m∠3 = 180° - 120° - 30° = 30°

Step 3: Solve for the missing side lengths

• *Note: SOH CAH TOA: sin =
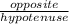  `(opposite)/(hypotenuse)`, cos =
  `(adjacent)/(hypotenuse)`, tan =
  `(opposite)/(adjacent)`
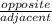
• x can be solved by using sine

1. The angle opposite of 90 is 60°, so
   `sin(60)=(90)/(x)`
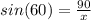
2. Then isolate x to one side,
   `x=(90)/(sin(60))`
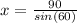
3. Finally solve for x, x ≈ 104 (means x is approximately 104)

• w can be solved by using sine

1. The angle opposite of w is 30° and the hypotenuse is 104, so
   `sin(30)=(w)/(104)`
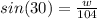
2. Then isolate w to one side,
   `w=104(sin(30))`
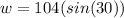
3. Finally solve for w, w = 52

• z can be solved by using cosine
• *Note: 30° + 30° = 60°

1. The angle adjacent to 90 is 60°, so
   `cos(60)=(90)/(z)`
2. Then isolate z to one side,
   `z=(90)/(cos(60))`
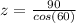
3. Finally solve for z, z = 180

• y can be solved by using cosine

1. The angle adjacent to y is 30° and the hypotenuse is 180, so
   `cos(30)=(y)/(180)`
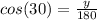
2. Then isolate y to one side,
   `y=180(cos(30))`
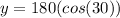
3. Finally solve for y, y ≈ 156 (means y is approximately 156)