Answer:
Approximately
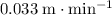 (meters per minute.)
(meters per minute.)
Step-by-step explanation:
Let
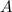 and
and
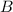 denote the bottom and top width of the trough, respectively. It is given that
denote the bottom and top width of the trough, respectively. It is given that
 and
and
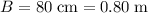 . Let
. Let
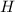 denote the height of this trough;
denote the height of this trough;
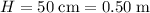 .
.
Let
 denote the current depth of the water in this trough.
denote the current depth of the water in this trough.
Let
 denote the current width of the surface of the water. As water fills the trough, this width increases from
denote the current width of the surface of the water. As water fills the trough, this width increases from
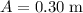 (width of bottom of trough) to
(width of bottom of trough) to
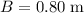 (width of top of trough.)
(width of top of trough.)
The relationship between
 and
and
 is linear:
is linear:
 .
.
Cross-section area of water in this trough:
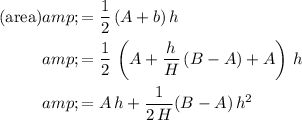 .
.
Let
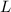 denote the length of this trough;
denote the length of this trough;
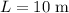 .
.
Let
 denote the volume of water in this trough:
denote the volume of water in this trough:
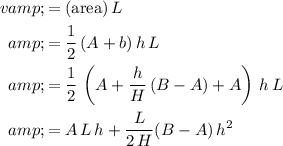 .
.
Differentiate both sides implicitly with respect to
 :
:
![\displaystyle (d)/(dv)[v] = (d)/(dv)\left[A\, L\, h + (L)/(2\, H)\, (B - A)\, h^(2)\right]](https://img.qammunity.org/2023/formulas/physics/high-school/ohchkosrddrhgqh8isgtvsjnfsavj0exlm.png) .
.
![\displaystyle (d)/(dv)[v] = (d)/(dv)[A\, L\, h] + (d)/(dv)\left[(L)/(2\, H)\, (B - A)\, h^(2)\right]](https://img.qammunity.org/2023/formulas/physics/high-school/5riighnbb7kf76frg9abbcww3wq47eegnj.png) .
.
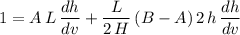 .
.
(Note that
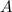 ,
,
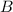 ,
,
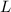 , and
, and
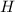 are constants.)
are constants.)
Rearrange this equation to obtain:
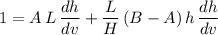 .
.
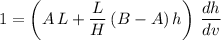 .
.
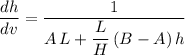 .
.
Let
 denote time. It is given that the trough is being filled at a rate of
denote time. It is given that the trough is being filled at a rate of
 . In other words:
. In other words:
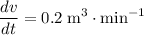 .
.
Apply the chain rule to find the rate at which
 is changing with respect to time
is changing with respect to time
 :
:
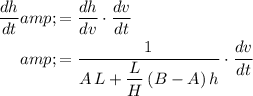 .
.
Substitute in
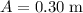 ,
,
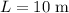 ,
,
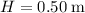 ,
,
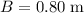 ,
,
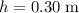 (converted from
(converted from
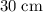 ), and that the rate of change in
), and that the rate of change in
 is
is
 :
:
 .
.
In other words, the depth of the water in this trough increases at a rate of approximately
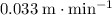 (meters per minute.)
(meters per minute.)