Question

The polynomial P(x) of degree 4 has

a root of multiplicity 2 at x = 4
• a root of multiplicity 1 at x = 0 and at x = -1
• It goes through the point (5,21)
Find a formula for P(x).
P(x) =
Question Help: Message instructor

Answer 1

P(x) = 0.7
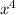`x^(4)` - 4.9x³ + 5.6x² + 11.2x

Explanation:

given a polynomial with roots x = a and x = b , then the factors are

(x - a) and (x - b)

If x = a is of multiplicity 2 then factor is (x - a)²

the polynomial is then the product of the factors

p(x) = a(x - a)(x - b) ← a is a multiplier

give x = 4 is a root with multiplicity 2 then (x - 4)² is the factor

x = 0 has factor (x - 0) , that is x

x = - 1 has factor (x - (- 1)) , that is (x + 1)

the polynomial is then the product of the factors

P(x) = ax(x + 1)(x - 4)² ← expand squared factor using FOIL

= ax(x + 1)(x² - 8x + 16)

= a(x² + x)(x² - 8x + 16) ← distribute

= a(
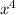`x^(4)` - 8x³ + 16x² + x³ - 8x² + 16x)

= a(
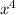`x^(4)` - 7x³ + 8x² + 16x)

to find a substitute (5, 21 ) into P(x)

21 = a(
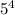`5^(4)` - 7(5)³ + 8(5)² + 16(5))

21 = a(625 - 875 + 200 + 80)

21 = 30a ( divide both sides by 30 )

0.7 = a

then

P(x) = 0.7(
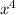`x^(4)` - 7x³ + 8x² + 16x) ← distribute parenthesis

P(x) = 0.7
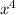`x^(4)` - 4.9x³ + 5.6x² + 11.2x