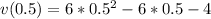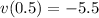Answer:
The velocity is - 5.5m/s
Step-by-step explanation:
Given
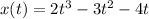
Required
The velocity when acceleration = 0
First, calculate the velocity (v)
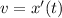
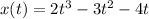 --- differentiate
--- differentiate
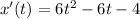
So:
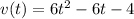
Next, calculate acceleration (a)
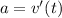
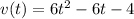 --- differentiate
--- differentiate
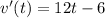
So:
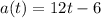
From the question acceleration = 0
So:
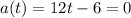
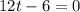
Solve for t
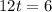
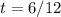
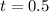
Substitute
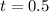 in
in
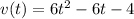 to get the velocity
to get the velocity