Step-by-step explanation:
Part A.
To get from D to E, we go 5 units right and 2 units up, then we can write the following equation to find the length DE
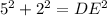
Solving for DE, we get
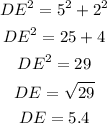
Therefore, DE = 5.4 units
Part B.
To get from D to F, we go 5 units right and 4 units down, so we can write the following equation to find the length of DF
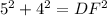
Solving for DF, we get
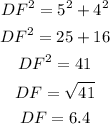
Therefore, the length of DF is 6.4 units
Part C.
Then, the perimeter is the sum of all the sides of the triangle, so
Perimeter = DE + DF + FE
Perimeter = 5.4 + 6.4 + 6
Perimeter = 17.8 units