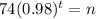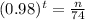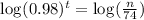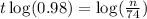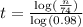Question

Scientists studying biodiversity of amphibians in a rain forest have discovered that the number of species is decreasing by 2% per year. Thereare currently 74 species of amphibians in the rain forest. Which logarithmic function models the time, f(n), in years, it will take the number ofspecies to decrease to a value of n?logo.skOA f(n) =OB. f(n) = logo.98oc f(n) = 1061.0274nOD. f(n) = 1057.02 )

Answer 1

`t=\frac{\log_{}((n)/(74))}{\log_{}(0.98)}`

Explanation:

The number of amphibians in the forest after t years can be given by an equation in the following format:

`N(t)=N(0)(1-r)^t`

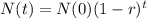
In which N(0) is the initial number of amphibians and r is the decrease rate, as a decimal.

Decreasing by 2% per year.

This means that r = 0.02.

There are currently 74 species of amphibians in the rain forest.

This means that N(0) = 74.

So

`N(t)=74(1-0.02)^t=74(0.98)^t`

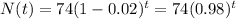
Which logarithmic function models the time, f(n), in years, it will take the number of species to decrease to a value of n?

This is t for which N(t) = n. So

`74(0.98)^t=n`
`(0.98)^t=(n)/(74)`
`\log _{}(0.98)^t=\log _{}((n)/(74))`
`t\log _{}(0.98)=\log _{}((n)/(74))`
`t=\frac{\log_{}((n)/(74))}{\log_{}(0.98)}`