Since the length of the fence is 500 feet, then
The perimeter of the rectangle is 500
If the width of the rectangle is x, and the length is y, then
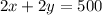
Divide each term by 2
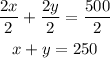
Subtract x from each side to find y in terms of x
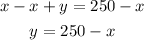
The width of the rectangle is x and the length is 250 - x
Now we can find the area of the rectangle
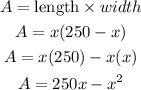
We will find the x-coordinate of the vertex of the quadratic using the rule down
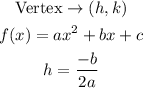
From the equation of the area, we will find a, and b to get h
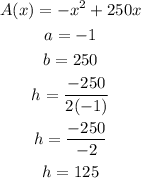
Then the x-coordinate of the vertex is 125 feet which makes the area maximum
Substitute x by 125 in the equation of the area
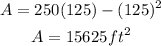
The maximum area is 15625 square feet