The formula of the surface area (SA) of a hexagonal prism is given by:
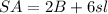
where B is the area of the hexagon, s the side of the hexagon, and l the length/height of the prism.
B is given by:

where a represents the apothem of the hexagon and P the perimeter.
Thus, we have to find the apothem in order to use the formula. If we divide the hexagon into six regular triangles, the vertex of the triangle in the center of the hexagon will have a 60º angle:
However, to be able to get the apothem what we need to do is a right triangle, for we have the measure of one angle and one side. Using the tangent trigonometric function we get:
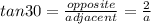
Solving for a:

Now that we have the apothem, we can use is in the formula to calculate the area:

Simplifying:
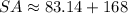
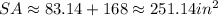
Answer: 251.14 in²