Step 1. The function P(x) that we have is:
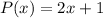
And the function that is dilated by is the function I(x) defined as follows:
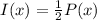
This means that we will be dilating the original function P(x) by 1/2.
Step 2. To find the function rule that represents I(x), we need to substitute P(x) into I(x):
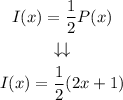
Step 3. Now we need to simplify this expression. For that, we multiply 1/2 by 2x and by 1:
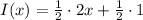
Simplifying the multiplications:

That is the function rule for I(x) and it is shown in the first option.
Answer:
