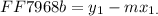If we say

then dividing both sides by (x - x_1) gives
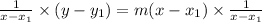
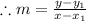
which is our answer!
The above equation correctly gives the slope m because it is in accord with the definition of m as rise / run.
(E).
Let us now expand the RHS of the first equation to get:

Adding y_1 to both sides gives
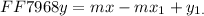
Or in a more neat form
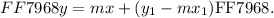
(F).
As can be seen from the equation y = mx + b we got in E, the y-intercept b is given by