Question

Solve the following system of equations6x+5y=−2−7x-9y=−23

Answer 1

The given system of equations is

`\begin{gathered} 6x+5y=-2\rightarrow(1) \\ -7x-9y=-23\rightarrow(2) \end{gathered}`

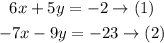
Multiply equation (1) by 7 and equation (2) by 6 to make the coefficients of x equal in values and different in signs to eliminate x

`\begin{gathered} 7(6x)+7(5y)=7(-2) \\ 42x+35y=-14\rightarrow(3) \end{gathered}`
`\begin{gathered} 6(-7x)-6(9y)=6(-23) \\ -42x-54y=-138\rightarrow(4) \end{gathered}`

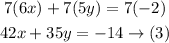
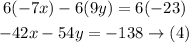
Add equations (3) and (4) to eliminate x

`\begin{gathered} (42x-42x)+(35y-54y)=(-14-138) \\ -19y=-152 \end{gathered}`

Divide both sides by -19 to find y

`\begin{gathered} (-19y)/(-19)=(-152)/(-19) \\ y=8 \end{gathered}`

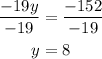
Substitute y by 8 in equation (1) to find x

`\begin{gathered} 6x+5(8)=-2 \\ 6x+40=-2 \end{gathered}`

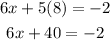
Subtract 40 from both sides

`\begin{gathered} 6x+40-40=-2-40 \\ 6x=-42 \end{gathered}`

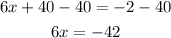
Divide both sides by 6 to find x

`\begin{gathered} (6x)/(6)=(-42)/(6) \\ x=-7 \end{gathered}`

The solution of the system is (-7, 8)