We know that a root of a quadratic function is a value of x that makes the function equal to 0.
So,
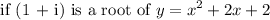
it must be fulfilled that,
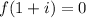
Now, we must replace (1 + i) in the function
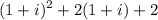
solving the parentheses,
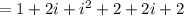
Using that i^2 = -1
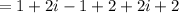
grouping similar terms
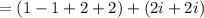
Finally, simplifying
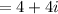
We can see that
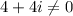
So, (1 + i) is not a root of the equation.
The statement is false.