Given directed line segments from (-10,-5) to (5,1) with ratio 1:2
The coordinate for the partition on the line segment is given by the formula
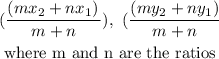
From the formula, let us define, all the parameters from the given coordinates and ratio
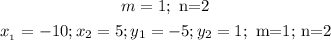
Substituting the parameters into the formula to the coordinate of the partition will give
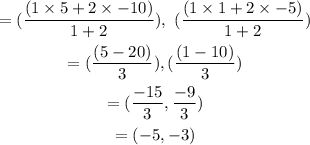
Hence, the coordinates of the point on the directed line segment that partitions the segment into the ratio 1 to 2 is (-5,-3)