In order to find the moment t, in seconds, when the bullet hits the ground, we need to use
h = 0
v₀ = 1120
in the given formula:
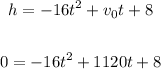
Now, we can solve the above equation using the quadratic formula:
![\begin{gathered} t=\frac{-1120\pm\sqrt[]{1120^2-4(-16)(8)}}{2(-16)} \\ \\ t=\frac{-1120\pm\sqrt[]{1254400+512}}{-32} \\ \\ t=\frac{-1120\pm\sqrt[]{1254912}}{-32} \\ \\ t=35\pm\sqrt[]{(2451)/(2)} \\ \\ t_1\cong70.01 \\ \\ t_2\cong-0.01 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pglmde8bw6x54eaz0zfn4ohezh6p9bvati.png)
Since the time must be positive, the answer is t₁. Therefore:
It will hit the ground after 70.01 seconds.