Let's start graphing the first inequality y > 3x - 4. Since this is already in its slope-intercept form, we can see right away that the y-intercept of its boundary line is at (0, -4) and the slope is 3.
Aside from the y-intercept, let's find another point on the line using the slope. We will add 3 on the y-coordinate of the y-intercept and add 1 on the x-coordinate.
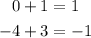
Hence, we have another point on the boundary line at (1, -1).
Let's plot these two points (0, -4) and (1, -1) and connect them using a dashed line since the inequality is "greater than". Also, the shade of the graph will be above the line.
The graph of the first inequality y > 3x - 4 is:
Moving on to the second inequality y ≤ x + 1, the y-intercept is at (0, 1) and the slope is 1.
Let's find another point on the line using the slope by adding 1 on the y-coordinate of the y-intercept and 1 on the x-coordinate.
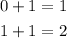
Therefore, we have another point on the line at (1, 2).
Let's plot these points (0, 1) and (1, 2) on the graph. Connect them using a solid line because the inequality symbol has "or equal to". The shade of the graph will be below the line since the inequality symbol is "less than".
The graph of the second inequality y ≤ x + 1 is:
Combining the two graphs, we have:
The solution to the two inequalities would be the common shaded region, hence, in the diagram, it will be the darker shade.
Based on the given choices, this is shown by Option D.