Question

Effective resistance for the entire circuit to the nearest whole number.

Answer 1

Remember that if two resistors are conected in series, the effective resistance of both of them is given by:

`R=R_1+R_2`

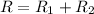
On the other hand, when two resistors are connected in parallel, the effective resistance of both of them is given by:

`(1)/(R)=(1)/(R_1)+(1)/(R_2)`

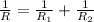
Notice that the resistors R₂ and R₃ are connected in parallel. Then, the effective resistance of that array is:

`\begin{gathered} (1)/(R_(2,3))=(1)/(R_2)+(1)/(R_3) \\ \\ =(1)/(6.00\Omega)+(1)/(13.00\Omega) \\ \\ =(13.00\Omega+6.00\Omega)/((6.00\Omega)(13.00\Omega)) \\ \\ =(19.00)/(78.00\Omega) \\ \\ \\ \Rightarrow R_(2,3)=(78.00\Omega)/(19)\approx4.1\Omega \end{gathered}`

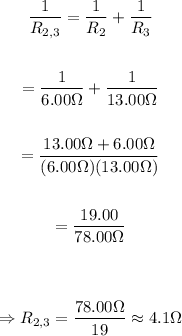
On the other hand, the array of resistors 2 and 3 is connected in series to the resistor 1. Then, the effective resistance is given by:

`\begin{gathered} R_(1,2,3)=R_1+R_(2,3) \\ \\ =1.00\Omega+4.1\Omega \\ \\ \therefore R_(1,2,3)=5.1\Omega\approx5\Omega \end{gathered}`

Therefore, the effective resistance of the entire circuit to the nearest whole number is 5Ω.