Question

find the distance between ivy’s house and the supermarket and the distance between the supermarket and the bank. each distance is rounded to the nearest meter.

Answer 1

The distance between the Supermarket and the bank is 854 meters

The distance between Ivy’s house and the Supermarket is 1,014 meters

Step-by-step explanation:

We were given the following information:

Pont A represents Ivy's house

Point B represents the Supermarket

Point C represents the Bank

`\begin{gathered} m\angle A=32^(\circ) \\ AB=c=? \\ BC=a=? \\ m\angle B=109^(\circ) \\ AC=b=1,523m \\ m\angle C=180-(109+32)=180-141=39^(\circ) \\ m\angle C=39^(\circ) \end{gathered}`

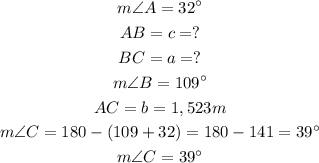
We were given 2 known angles and 1 known side. We will thus solve using Sine Rule as shown below:

`\begin{gathered} (Sin(A))/(a)=(Sin(B))/(b)=(Sin(C))/(c) \\ (Sin(32^(\circ)))/(a)=(Sin(109^(\circ)))/(1,523) \\ \text{Cross multiply, we have:} \\ a* Sin(109^(\circ))=1,523* Sin(32^(\circ)) \\ a=(1,523* Sin(32^(\circ)))/(Sin(109^(\circ))) \\ a=853.57\approx854 \\ a=854m \end{gathered}`

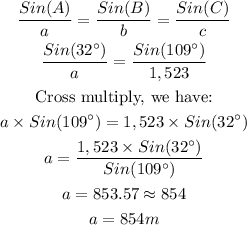
Therefore, the distance between the Supermarket and the bank is 854 meters

We will proceed further:

`\begin{gathered} (Sin(A))/(a)=(Sin(B))/(b)=(Sin(C))/(c) \\ (Sin(39^(\circ)))/(c)=(Sin(109^(\circ)))/(1,523) \\ \text{Cross multiply, we have:} \\ c* Sin(109^(\circ))=1,523* Sin(39^(\circ)) \\ c=(1,523* Sin(39^(\circ)))/(Sin(109^(\circ))) \\ c=1,013.68\approx1,014 \\ c=1,014m \end{gathered}`

Therefore, the distance between Ivy’s house and the Supermarket is 1,014 meters