Take into account that the period of a pendulum is given by the following formula:
![T=2\pi\sqrt[]{(l)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/ti4z4u7ndiirdgprizoi3aj3w92g8dmz1l.png)
where,
l: length = 2.3 m
g: acceleration of gravity = ?
T: period
The period T is:
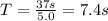
If you solve for g the equation of the period, you obtain:
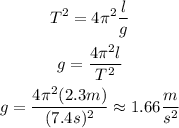
Hence, the acceleration of gravity at the location of the pendulum is approximately 1.66m/s^2