Question

How do I solve this rational equation in the form of a proportion?

Answer 1

`\text{ From least to greatest, the solutions are x=-4 and x=-8.}`

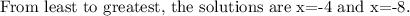
Explanation:

As a first step do cross multiplication and expand:

`\begin{gathered} x-2=(x+10)(x+3) \\ x-2=x^2+3x+10x+30 \end{gathered}`

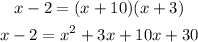
Organize the equation as the standard form of a quadratic equation:

`ax^2+bx+c=0`

Then, organizing the equation:

`\begin{gathered} x^2+12x+32=0 \\ \end{gathered}`

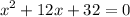
To solve a quadratic equation, use the quadratic formula:

`x=(-b\pm√(b^2-4ac))/(2a)`

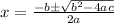
Hence, for the quadratic equation above, identify a,b, and c:

a=1, b=12, and c=32.

`\begin{gathered} x_1=(-12+√(12^2-4(1)(32)))/(2(1))=-(8)/(2)=-4 \\ x_2=(-12-√(12^2-4(1)(32)))/(2(1))=-(16)/(2)=-8 \end{gathered}`